Joseph Webber
About Me
I am a Zeeman Lecturer (equivalent to a fixed-term Assistant Professor position) at the Warwick Mathematics Institute at the University of Warwick. Prior to this, I was a postdoctoral research fellow (2024-2026) in the group of Professor Tom Montenegro-Johnson on the Leverhulme-funded project Shape Transforming Active Matter. Before that, I was a PhD student in the Department of Applied Mathematics and Theoretical Physics at the University of Cambridge, supervised by Professor Grae Worster. My PhD thesis, entitled Dynamics of super-absorbent hydrogels, is available here.
I’m an applied mathematician working at the interface between fluid mechanics and soft matter, specifically studying poroelasticity (the behaviour of porous, deformable media). I have a particular interest in hydrogels, soft elastic solids formed of a polymer matrix surrounded by water molecules, and their swelling and drying behaviour. The publications below or my CV show more details on what I’ve been working on, but don’t hesitate to get in touch if you have any questions.
To view resources related to teaching, follow the link.
The UK Hydrogels Network now has a website - join the hydrogels mailing list for researchers working on hydrogels in the UK to stay up-to-date.
Publications
-
Physical Review Fluids (2025) 10:100501Self-oscillating gels are chemically-responsive hydrogels coupled to an oscillating chemical reaction of a stimulus solute. In response to the oscillating solute concentration field, responsive gels periodically swell and deswell, expelling their adsorbed water as they transition to a drier state, and reswelling once they return to a hydrophilic state. This volume phase transition occurs when the local stimulus concentration crosses a critical value...
doi.org/10.1103/52bv-vyb5
-
Physical Review Research (2025) 7:L032055Responsive hydrogels can sense environmental stimuli and respond as actuators by expelling water and changing shape. In this article, we develop theory to demonstrate that groups of responsive hydrogels can also communicate with each other, by utilising the effect of elastic deformation on chemical reaction dynamics. Specifically, we consider a system of two spatially-separated chemically responsive hydrogels...
doi.org/10.1103/xbvn-5b59
-
Journal of Fluid Mechanics (2025) 1009:A38Thermo-responsive hydrogels are smart materials that rapidly switch between hydrophilic (swollen) and hydrophobic (shrunken) states when heated past a threshold temperature, resulting in order-of-magnitude changes in gel volume. Modelling the dynamics of this switch is notoriously difficult, and typically involves fitting a large number of microscopic material parameters to experimental data. In this paper, we present and validate an intuitive, macroscopic description of responsive gel dynamics and use it to explore the shrinking, swelling and pumping of responsive hydrogel displacement pumps...
doi.org/10.1017/jfm.2025.249
-
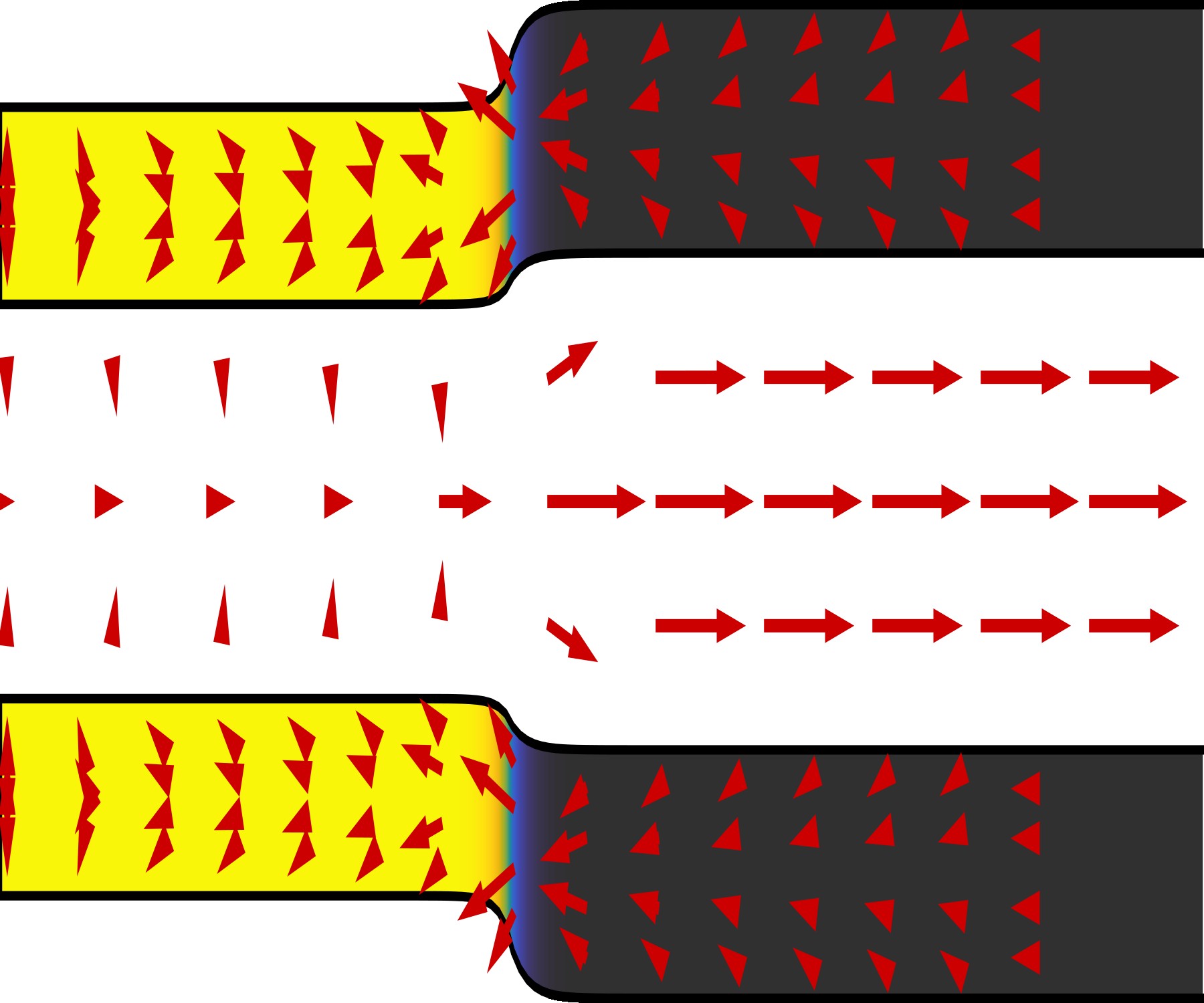
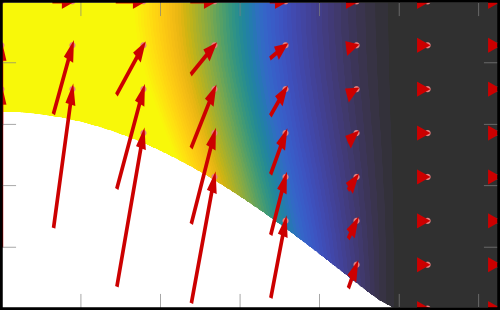Proceedings of the Royal Society A (2025) 481:20240721Recent experiments have shown a rich variety of behaviour when soft, brittle, hydrogels are frozen, since water cannot freeze within the pore space of these materials as a result of the Gibbs-Thompson effect. Hence, no ice forms within the hydrogel matrix, and pure ice grows by cryosuction, drawing water from the surrounding gel towards the phase boundary. The growth of this ice...
doi.org/10.1098/rspa.2024.0721
-
PhD thesis: University of CambridgeThis thesis explores the behaviour of hydrogels, a broad class of materials comprising a hydrophilic polymer scaffold surrounded by adsorbed water molecules, potentially comprising over 99% water by volume. In general, hydrogels are soft, elastic, porous materials that can swell or dry to a significant degree by imbibing...
doi.org/10.17863/CAM.109003
-
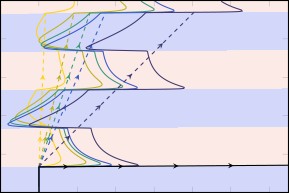
Physical Review E (2024) 109:044602We investigate the formation of wrinkling instabilities at the interface between layers of hydrogel and water, which arise to relieve horizontal compressive stresses caused by either differential swelling or confinement. Modelling the gel using a linear-elastic-nonlinear-swelling approach, we determine both a criterion for marginal stability and the growth rates of normal modes. Furthermore, our formulation...
doi.org/10.1103/PhysRevE.109.044602
-
Journal of Fluid Mechanics (2023) 960:A38We consider the multidirectional swelling and drying of hydrogels formed from super-absorbent polymers and water, focusing on the elastic deformation caused by differential swelling. By modelling hydrogels as instantaneously incompressible, linear-elastic materials and considering situations in...
doi.org/10.1017/jfm.2023.201
-
Journal of Fluid Mechanics (2023) 960:A37We introduce a new approach for modelling the swelling, drying and elastic behaviour of hydrogels, which leverages the tractability of classical linear-elastic theory whilst incorporating nonlinearities arising from large swelling strains. Relative to a reference state of a fully swollen gel, in which the polymer scaffold may only comprise less than...
doi.org/10.1017/jfm.2023.200
-
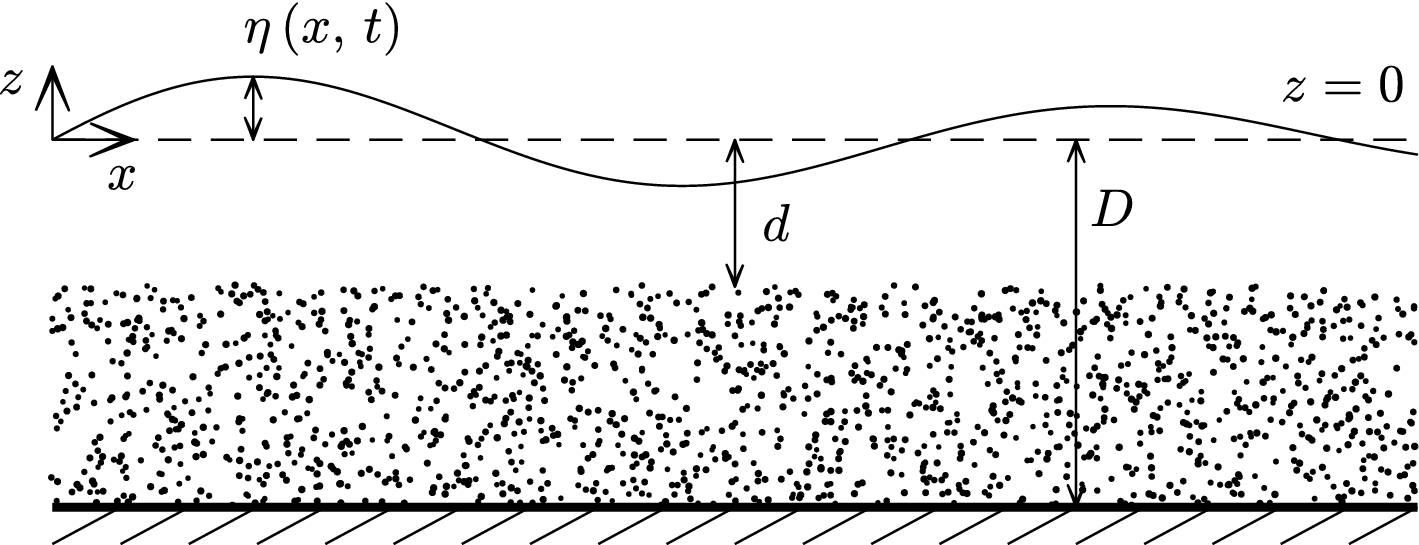Environmental Fluid Mechanics (2021) 21:1119-1135Motivated by shallow ocean waves propagating over coral reefs, we investigate the drift velocities due to surface wave motion in an efectively inviscid fuid that overlies a saturated porous bed of fnite depth. Previous work in this area either neglects the large-scale flow between layers...
doi.org/10.1007/s10652-021-09811-8
-
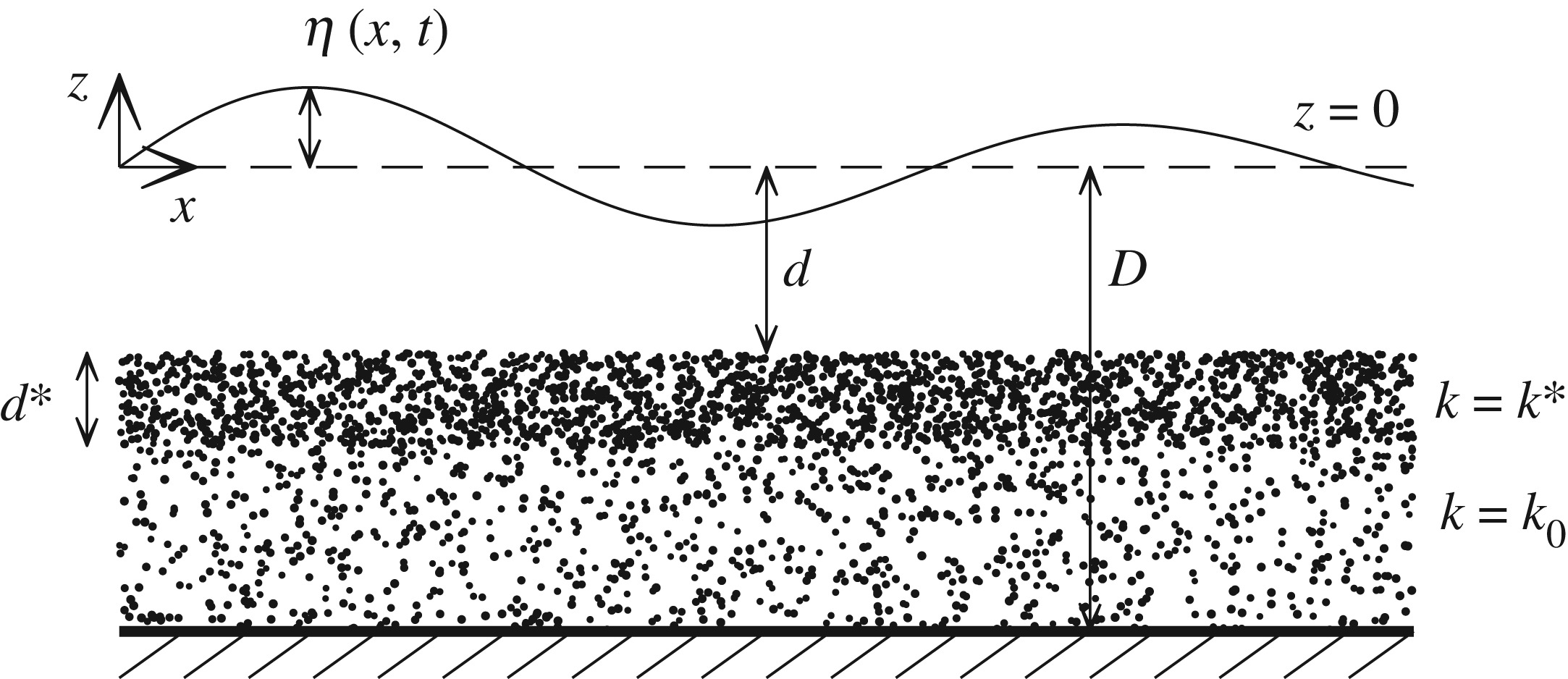Philosophical Transactions of the Royal Society A (2020) 378:20190531In his famous paper of 1847 (Stokes GG. 1847 On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 8, 441-455), Stokes introduced the drift effect of particles in a fluid that is undergoing wave motion. This effect, now known as Stokes drift, is the result of differences between the Lagrangian and Eulerian velocities...
doi.org/10.1098/rsta.2019.0531
-
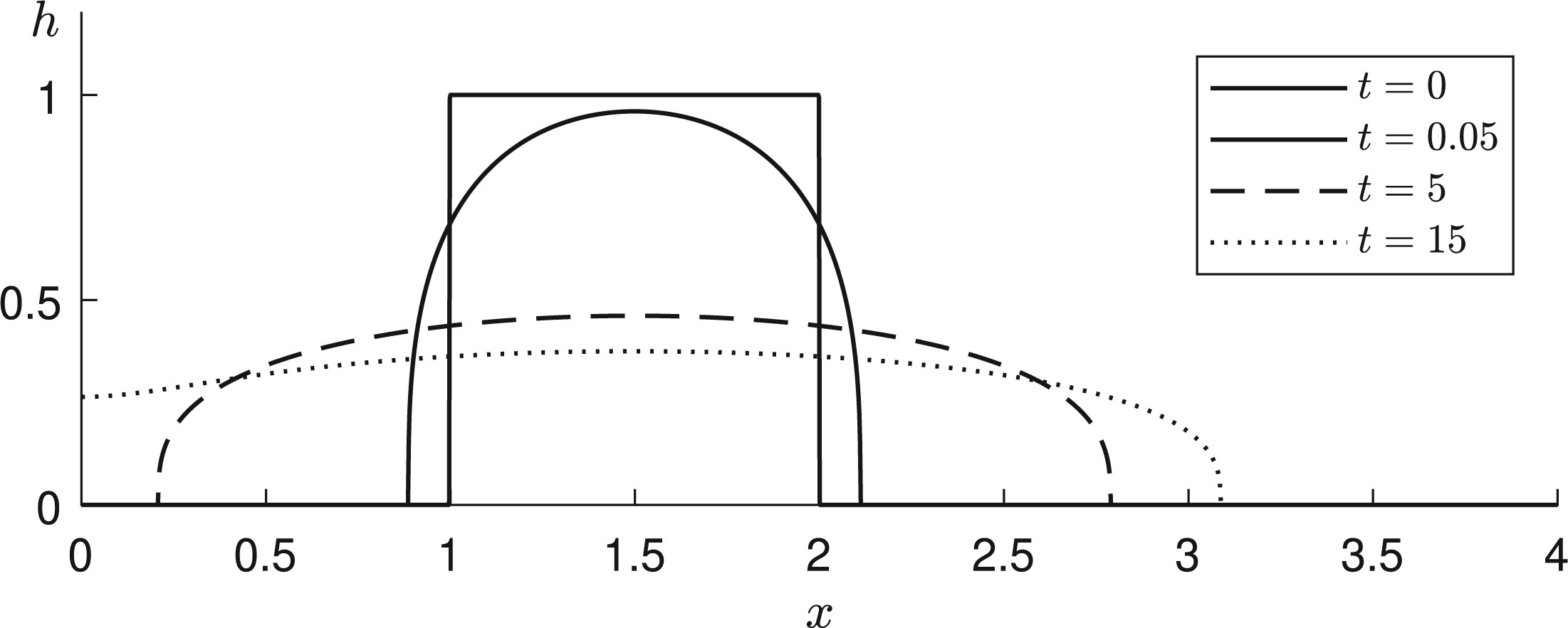Quarterly Journal of Mechanics and Applied Mathematics (2020) 73:1-23In a recent article, Ball and Huppert (J. Fluid Mech., 874, 2019) introduced a novel method for ascertaining the characteristic timescale over which the similarity solution to a given time-dependent nonlinear differential equation converges to the actual solution, obtained by numerical integration, starting from given initial conditions. In this article, we apply this method to a range of different partial differential equations...
doi.org/10.1093/qjmam/hbz019
Talks and posters
-
A linear-elastic-nonlinear-swelling model for hydrogels
Abstract
Hydrogels are an important example of poroelastic materials, formed from hydrophilic polymer chains surrounded by adsorbed water molecules. Key to many of their uses is the fact that they can swell to hundreds of times their initial size upon imbibition of water, but at any swelling state they behave as solid, soft, elastic media. Modelling such gels can be challenging: large-strain elasticity arising from swelling and drying must be incorporated alongside the interaction between water and polymer molecules and the transport of water through the pore spaces. This has, in the past, led to many complicated nonlinear approaches based on an understanding of the molecular-scale behaviour. In this talk, I will summarise a model for the dynamics of hydrogels that treats them as instantaneously incompressible linear-elastic materials, whilst allowing for nonlinearities in the isotropic strains corresponding to swelling. This approach is not only analytically tractable, but also able to describe the gel using only three (macroscopic) swelling-state-dependent material parameters and can be adapted to model responsive or active gels. I will then discuss further extensions of this approach to problems involving freezing and thermo- and chemo-responsive hydrogels.
-
A tractable framework for modelling hydrophilic large-swelling gels
Abstract
Developing models for super-absorbent gels is an important pursuit - materials formed from a porous elastic scaffold that can increase in volume by up to hundreds of times upon the uptake of water are found in fields as disparate as materials science, biomedical sciences (where such gels provide good analogues for biological tissues) and geophysics. Such models, however, typically fall into one of two categories: either they are based on linear poroelasticity and therefore fail to capture the large swelling strains that permit order-of-magnitude volume changes, or they rely on difficult-to-parameterise nonlinear elasticity: amongst other things, these models lose the tensorial nature of linear poroelasticity, can be analytically intractable, focus on steady states instead of transients, and often tend to disguise the dominant physics driving behaviour. In this talk, I will outline the linear-elastic-nonlinear-swelling (LENS) theory which allows for nonlinearities in swelling strains whilst linearising small deviatoric strains, in effect treating these gels as linear poroelastic materials with properties that change as they swell or dry. Gel dynamics are described by a nonlinear advection-diffusion equation, and it becomes possible to straightforwardly infer the transient shape of gels as they hydrate or dehydrate. This model has numerous benefits that make it suitable to accurately describe the response of gels, can couple neatly with fluid flows and explain a number of phenomena observed in experiments. From this starting point, I will show how a nonlinear poroelastic model like LENS can be incorporated in multiphysics problems including in modelling the freezing of porous media and outline recent work where it is extended to describe responsive hydrogels that swell or deswell as a result of external environmental triggers.
-
Poromechanical modelling of pumping with responsive hydrogels
Abstract
Responsive hydrogels undergo significant changes in volume as a result of changes in their local environment, be this through changing temperatures (e.g. PNIPAM gels), chemical concentrations, or light levels. These volume changes arise as the affinity of polymer chains for water molecules varies in response to external stimuli, and water is either driven into our out of the polymer network. As a result, responses can be slow, mediated by the viscously-dominated diffusion of water through the nanoporous gel scaffold, with centimetre-scale gels taking of the order of hours to reconfigure as their environment changes. Modelling these materials can be a challenge, and often relies on fitting a large number of microscopic material parameters to experimental data. We introduce an extension of the linear-elastic-nonlinear-swelling (LENS) model to describe responsive gels, allowing us to quantify the transient behaviour of thermo-responsive gels once the threshold temperature for deswelling is crossed, and the magnitude and direction of the flows of interstitial water that drive the reconfiguration. This framework allows us to move on to produce displacement pumps that react on much shorter timescales than similarly-sized responsive gels. These pumps operate by driving fluid radially out of thin tube walls, shrinking in response to temperature change, which in turn drives a flow along the lumen of the tube, unimpeded by the strong viscous resistance in the pore spaces. Modelling such devices requires us to understand the coupling between external fluid flows, gel dynamics, heat transfer and elasticity, but we illustrate how the gel and fluid dynamics problems can be uncoupled to allow for a more straightforward semi-analytic solution. In this talk, we discuss the main qualitative insights of our modelling of such devices and how such novel, model-inspired, geometries allow for the creation of devices that respond to external stimuli on tunable timescales, unlocking new possibilities for dynamic shape change.
-
How to prepare and present maths posters
Abstract
This talk, an updated and improved version of that given in 2024, was given to summer undergraduate students taking part in the SUMR scheme to introduce them to academic posters.
-
Getting stressed about frozen gels (IMA Lighthill-Thwaites Prize finalist 2025)
Abstract
When exposed to temperatures below freezing, we are all familiar with the damage that can occur to porous materials as ice forms - be this in the formation and growth of potholes in tarmac or the altogether disappointing experience that are frozen strawberries. It's commonly believed that the expansion of water as it freezes drives the buildup of stresses in the pore matrix, but for years it has been known that these stresses are far too small, and that actually a process called 'cryosuction', where the formation of ice draws water from the pores to rapidly grow even bigger chunks of pure ice, is the main driving factor behind this damage. Hydrogels - squishy, elastic, yet porous materials - provide the ideal media to understand the interplay between ice growth, elastic deformation and interstitial fluid flows when freezing is instigated, providing for the first time a complete mathematical model for the origin of shear and normal stresses driving this damage to deformable porous media. Owing to the small pore size, ice cannot form within the nanometre-scale gaps in a gel, but instead grows at a cooled boundary, sucking water through the gel and drying it out, until eventually a steady state of stressed, deswollen, gel adjacent to pure ice is formed. Understanding how the deswollen gel that is left behind is sheared and squeezed gives key insights into a number of problems, including the cryopreservation of human organs for transplant.
-
Freezing of hydrogels: modelling cryosuction, deformation and ice growth
Abstract
When hydrogels - soft, porous materials formed from cross-linked polymer chains surrounded by adsorbed water molecules - are brought below freezing temperatures, water does not freeze in place inside the pores of the gel scaffold, and is instead expelled out of the hydrogel, forming pure ice. The gel that is left behind deswells and, as a result, stresses build up, impacting the mechanical response of the gel, the pressure exerted on the ice, and the transport of water through the gel towards the freezing front ('cryosuction'). In this talk, motivated by recent experiments carried out at ETH Zurich, I will show how mathematical models can give deep insight into the processes driving the formation of ice and deswelling of the hydrogel, both of which are inextricably linked. Understanding these processes firstly gives insight into the properties of the hydrogel itself - when a gel is frozen, eventually a steady state is reached wherein osmotic pressures exerted by the partially-dried hydrogel depress the liquidus temperature at the phase boundary sufficiently that no more ice can form. This is the basis for 'gel-freezing osmometry' and can be used to probe the micro-scale structure of hydrogels without seeking a sometimes-complex understanding of the polymer chains and their interactions with water molecules. Secondly, hydrogels provide excellent analogues for other deformable porous media as they are frozen, such as porous asphalt on road surfaces and soft fruits or even human organs. I will illustrate how continuum-mechanical models based on our recent 'LENS' (linear-elastic-nonlinear-swelling) approach can quantify the fluid flows, deformation and stress buildup inside squishy materials when they freeze, allowing us to mitigate any resulting damage through controlling the growth of large chunks of pure ice.
-
Modelling hydrogels at both ends of the temperature spectrum
Abstract
In this talk, I will discuss some recent work on theoretical models for two different ways in which hydrogels are affected by changes in temperature. At the colder end of the spectrum, freezing hydrogels provides insight into the damage of soft porous media through freeze-thaw cycles and the accumulation of stress that results when pure ice forms and the deswollen gel that is left behind compacts. Motivated by experiments performed here at ETH, I will show how a straightforward macroscopic model for gel deformation can successfully reproduce the results from these experiments, providing a much clearer physical justification for the processes driving gel deformation and damage than many models built on polymer-water interaction dynamics. Importantly, our model makes it clear how the qualitative nature of stress-induced fracture or damage is dependent on the physical confinement of the gel as opposed to temperature, degree of swelling, or material properties. At warmer temperatures, modelling thermo-responsive hydrogels, where deswelling occurs when the temperature crosses a critical threshold, can be a challenging task. The physics that drives this phase transition is hard to characterise macroscopically and the transition between 'cool' and 'hot' states involves the coupled transport of fluid through the pores and the elastic deformation of the scaffold that is left behind. Furthermore, exotic behaviour can be seen whereby sharp deswelling or reswelling fronts propagate through the gel even if heated gently above the threshold temperature. I will outline how the same modelling approaches as used to treat the freezing problem can unlock applications in microfluidic pumps and soft robotics, and how insight into the transition from swollen to deswollen states is just as important as knowledge of these states themselves when considering these potential applications.
-
Smart responsive gels: designing the building blocks of squishy bio-inspired devices
Abstract
Informal talk given as part of a MIRAW day
-
XOXO, Gossip Gel: oscillating chemical reactions facilitate communication between responsive hydrogels
Abstract
Responsive hydrogels promise a new world of soft and smart devices that interact with environmental stimuli, such as light-levels, ambient pH, and temperature. In pH-responsive gels, a chemical signal can result in a dramatic shape change which, in turn, squeezes solute out of the gel. This can locally change chemical concentrations, mediating long-distance signalling between isolated hydrogels. In this talk, I will discuss how coupling an oscillating chemical reaction to a chemo-responsive hydrogel leads to regular repeated shape changes, with the resultant release of solute feeding back into the reaction rate, allowing two spatially-separated hydrogels to “communicate” via synchronisation of their separate chemical reactions. This chemical signalling leading to a physical change allows us to view active gels as proxies for simple life and giving insights into ways in which colonies of microorganisms can signal to each other.
-
Smart responsive gels: designing the building blocks of squishy bio-inspired devices
Abstract
Invited talk given to the Mathematical Biology group at UCL
-
How to make a poster ...also how you shouldn't, why you should care, and how they matter
Abstract
This talk was given to summer undergraduate students taking part in the SUMR scheme to introduce them to academic posters.
-
A linear-elastic-nonlinear-swelling theory for hydrogels
Abstract
The talk given at Bristol on the 3rd of July was a subset of this longer talk given in Manchester on the 17th of May.
-
Freezing soft porous gels
Abstract
Soft or brittle materials are easily damaged by the action of freezing, and it is often argued that this damage arises as a result of water expanding as it freezes. Though this does have an effect, recent research has further highlighted the importance of a second mechanism, cryosuction, dominant in the case of porous media, where the freezing point of water is lowered by surface tension and water is drawn through the pores of the material. In this talk, motivated by experiments freezing hydrogels, we couple a model for cryosuction with modelling of the elastic and osmotic response of the gel, highlighting the mechanisms by which cracks can form and the material deforms. Our model allows us to precisely quantify the stresses and strains induced by ice formation, and also the rate of ice growth. This provides an analogue for the damage to soft tissues when frozen and could provide new insights into how to mitigate the effect.
-
A linear-elastic-nonlinear-swelling model for hydrogels
Abstract
Hydrogels are an important example of poroelastic materials, formed from hydrophilic polymer chains surrounded by adsorbed water molecules. Key to many of their uses is the fact that they can swell to hundreds of times their initial size upon imbibition of water, but at any swelling state they behave as solid, soft, elastic media. Modelling such gels can be challenging: large-strain elasticity arising from swelling and drying must be incorporated alongside the interaction between water and polymer molecules and the transport of water through the pore spaces. This has, in the past, led to many complicated nonlinear approaches based on deriving a free energy density from a bottom-up understanding of the molecular-scale dynamics. In this talk, I will summarise a new model for the dynamics of hydrogels that treats them as instantaneously incompressible linear-elastic materials, whilst allowing for nonlinearities in the isotropic strains corresponding to swelling. This approach is not only analytically tractable, but also able to describe the gel using only three (macroscopic) swelling-state-dependent material parameters. I will discuss the new predictions that such a model can make and show how the aforementioned material parameters for any gel could be easily determined experimentally.
-
Buckling and swelling instabilities of super-absorbent gels
Abstract
The formation of a wrinkled pattern on the surface of hydrogels as they are brought into contact with water and begin to swell is a familiar phenomenon discussed extensively in the literature, and leads to a wide array of behaviours as the gel continues to swell. The 'reticulated' wrinkle pattern can coarsen, crease, fold or even disappear entirely as more and more water is drawn in to the gel scaffold, but studies usually only focus on the criteria for the exchange of stability. In this talk, I introduce how a linear stability analysis for the onset of stability can be carried out in a poroelastic framework, with different mechanisms for patterning at different times.
At early stages, when only a thin skin on the surface of the gel is swollen, buckling occurs as a purely elastic phenomenon, with horizontal compressive stresses competing against anchoring from the base of the gel to form the pattern. This is then seen to smooth out at the same rate as the growth of the boundary layer, an observation that can be explained in terms of classical plate theory. At late stages, however, I show that wrinkling can only occur with volumetric change, and pattern formation is swelling-dominated. Understanding these two distinct processes allows us to describe observations of patterning made in experiments, including criteria for transient instabilities that disappear entirely as the gel approaches its steady, swollen, state.
-
Wrinkling instabilities of swelling hydrogels
Abstract
It has long been known that gels attached to a solid surface and brought into contact with water can form wrinkles, and this has often been explained as resulting from an elastic instability akin to Euler's analysis of buckling beams. However, experiments also show that the characteristic wavelength of wrinkles increases in time and, in some cases, they are seen to smooth out entirely as the hydrogel approaches its steady state. We use our linear-elastic-nonlinear-swelling model to conduct a linear stability analysis of the interface and calculate growth rates of normal modes. We find that, unlike the Euler beam, there are no incompressible instabilities when the gel is tethered to a rigid base and that elastically-driven instabilities are limited by water transport through the gel. If the base state itself is differentially swollen, such as when a gel is first exposed to water, we find a different, osmotically-driven, instability, and the interplay between osmotically-driven flow and elasticity selects a wavelength that scales with the thickness of the swollen region. As the base state approaches its uniform steady state, the characteristic wavelength increases and the effect of this latter mechanism becomes less important, reducing the growth rate and smoothing the wrinkles.
-
Linear stability analysis for the formation of wrinkles on confined swelling hydrogels
Abstract
Wrinkling, buckling and creasing instabilities are some of the most familiar phenomena observed in the study of soft materials including hydrogels. They arise when there is mechanical confinement, for example from a fixed base or from hoop stresses in swelling spheres, leading to the preferential formation of wrinkles to relieve shear stresses from the confining strain. These have long been studied as purely elastic instabilities, with a mechanism akin to Biot's classic stability analysis of an elastic half-space under pre-stress. Here, we argue that the swelling process itself is a key part of the mechanism driving these instabilities by carrying out a linear stability analysis of the swelling of a finite layer of gel under horizontal confinement. This stability analysis uses our own linear-elastic-nonlinear-swelling theory for hydrogels that captures the nonlinearities arising from the large isotropic strains when a gel takes on water but allows for an analytically tractable approach through linearising around small deviatoric strains. Under this theory, the physical processes driving the swelling and drying that forms the wrinkles can be easily seen, unlike in fully nonlinear approaches where only a condition for marginal stability can be derived through minimisation of free energy. Furthermore, the growth rate of a given instability is deduced, allowing us to determine the separate influences of wavenumber, layer thickness and material properties on the stability of the water-gel interface. It is observed that the anchoring effect of the fixed base of the gel layer stabilises low-wavenumber (long-wavelength) wrinkles, whilst the growth rate increases unboundedly with the wavenumber, leading to an 'ultraviolet catastrophe' whereby infinitesimally small wavenumbers grow at an infinite rate. We propose solving this by introducing a surface tension at the gel-water interface that serves to stabilise short-wavelength instabilities. The effect of this surface tension is quantified for two different mechanisms; firstly, a surface tension that arises as a bulk elastic discontinuity in stress, and secondly as one arising from a discontinuity in the pore pressure of water between the liquid and gel phases. Quantitative differences between these two mechanisms are discussed, and the evolution of the most unstable wavenumber in time is evaluated and compared to the smoothing and healing of these instabilities seen in experiments, where wrinkles are known to coarsen and, in some cases, disappear entirely as the gel layer imbibes more water. We show that our theory, with the addition of surface tension, can describe all these observations and postulate how further experimentation could determine the true physical origin of the surface tension at the interface.
-
A linear-elastic-nonlinear-swelling theory for hydrogels: displacements and differential swelling
Abstract
The shapes of hydrogels as they swell or dry in one spatial dimension, for example when a bead of gel is placed in water, can be determined straightforwardly using polymer conservation. For problems in higher dimensions, we derive an expression for the displacement field of individual gel elements, which allows us to describe the shape of arbitrarily complicated gel geometries given the polymer-fraction field. In a result with parallels in classical linear elasticity, we find that the displacement field satisfies a biharmonic equation forced by gradients in the polymer fraction. As a demonstration, we investigate the drying of slender cylinders of hydrogel by evaporation into the air, with their bases submerged in reservoirs of water. At leading order, the gel locally contracts isotropically as it loses water, with the deviatoric shrinkage arising from differential drying remaining small. Experiments show the formation of a concave top surface and convex bottom surface, phenomena that are explained qualitatively by our model. We also show how our results are equivalent to a mathematical description of the cylinders as stacked disks, with each disk satisfying equations of classical plate theory and coupled dynamically to the disks above and below it.
-
Multidirectional gel swelling and drying: a linear-elastic-nonlinear-swelling theory for hydrogels
Abstract
Super-absorbent polymers can form hydrogels with polymer fractions of under 1% by volume when placed in water, with the water molecules being adsorbed by the hydrophilic polymer to form an elastic material. This water is not fixed in place: the polymer scaffold creates a porous structure through which the water can flow to drive swelling and drying processes. Existing studies of the behaviour of these two-phase materials tend to either rely on poroelasticity, coupling the interstitial flow with a constitutive relation to describe the deformation stresses on the gel, or use a microscopic chemical understanding of the water-polymer interactions, minimising the energy density to find both the steady and transient swelling states. In our work, we have derived a constitutive and dynamic model which allows for nonlinearity in the swelling strains but linearises around the macroscopic elastic behaviour of the gel, in effect treating such hydrogels as instantaneously linear-elastic. For one-dimensional problems, such as a gel sphere swelling in water, the swelling state can be described fully by the polymer fraction, which also gives the radial extent of the sphere through a polymer conservation constraint. However, in higher-dimensional problems, the polymer fraction alone cannot describe the gel, since there may be differential swelling in different directions. In such cases, we illustrate how an equation can be derived to describe the displacement field for the gel, which is seen to satisfy a modified biharmonic equation forced by the polymer fraction field, a direct analogue of the biharmonic equation for the displacement field as seen in linear elastostatics. Relying solely on the founding assumption of small deviatoric strains, we can determine the shape of a gel as it is allowed to swell and dry, as well as the transient state as water flows throughout. As an illustration of the utility of this approach, the problem of a cylinder, with its base immersed in water, drying in the air, is considered. In this situation, there is both radial shrinkage and shrinkage along the axis of the cylinder, with the top of the cylinder drying to a greater extent than the base as water is drawn up and evaporated away, with such a problem requiring more than just a polymer fraction for a full description. These modelling assumptions are shown to result in a description of the gel which both agrees with experiments and with a Lagrangian description of the differential drying of the cylinder as a series of stacked elastic plates. Experiments have shown that the cylinder becomes concave on its top surface and convex at its base before reaching a steady state, and both of these phenomena can be described using this displacement formulation, providing further evidence of its ability to solve these more complicated problems.
-
Powered by Jekyll and Minimal Light theme.